A mathematical shortcut for determining quantum information lifetimes
A new, elegant equation allows scientists to easily compute the quantum information lifetime of 12,000 different materials.
Scientists have uncovered a mathematical shortcut for calculating an all-important feature of quantum devices.
Having crunched the numbers on the quantum properties of 12,000 elements and compounds, researchers have published a new equation for approximating the length of time the materials can maintain quantum information, called “coherence time.”
“People have had to rely on complicated codes and calculations to predict spin qubit coherence times. But now people can compute the prediction by themselves instantaneously. This opens opportunities for researchers to find the next generation of qubit materials by themselves,” said study co-author Shun Kanai of Tohoku University.
The elegant formula allows scientists to estimate the materials’ coherence times in an instant—versus the hours or weeks it would take to calculate an exact value.
The team, comprising scientists at the U.S. Department of Energy’s (DOE) Argonne National Laboratory, the University of Chicago, Tohoku University in Japan and Ajou University in Korea, published their result in April in the Proceedings of the National Academy of Sciences.
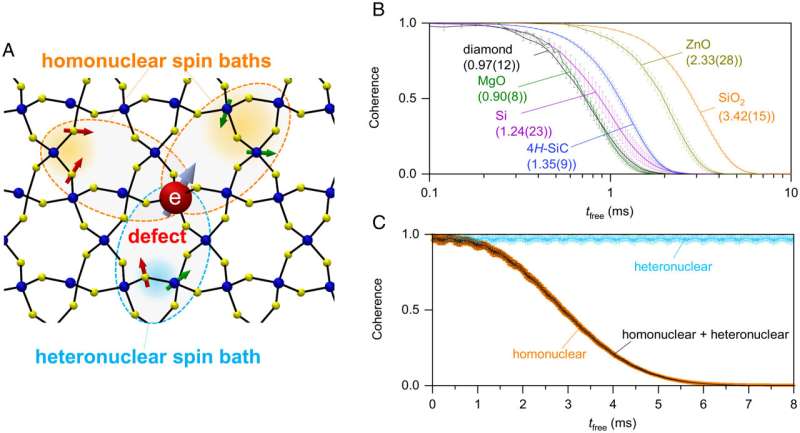
The team’s equation applies to a particular class of materials—those that can be used in devices called spin qubits.
“People have had to rely on complicated codes and calculations to predict spin qubit coherence times. But now people can compute the prediction by themselves instantaneously,” said Kanai. “This opens opportunities for researchers to find the next generation of qubit materials by themselves.”
Qubits are the fundamental unit of quantum information, the quantum version of classical computer bits. They come in different forms and varieties, including a type called the spin qubit. A spin qubit stores data in a material’s spin—a quantum property inherent in all atomic and subatomic matter, such as electrons, atoms and groups of atoms.
Scientists expect that quantum technologies will be able to help improve our everyday lives. We may be able to send information over quantum communication networks that are impenetrable to hackers, or we could use quantum simulations to speed up drug delivery.
The realization of this potential will depend on having qubits that are stable enough—that have long enough coherence times—to store, process and send the information.
While the research team’s equation gives only a rough prediction of a material’s coherence time, it gets pretty close to the true value. And what the equation lacks in precision, it makes up for in convenience. It requires only five numbers—the values of five particular properties of the material in question—to get a solution. Plug them in, and voila! You have your coherence time.
Diamond and silicon carbide are currently the best-established materials for hosting spin qubits. Now scientists can explore other candidates without having to spend days calculating whether a material is worth a deeper dive.
“The equation is like a lens. It tells you, ‘Look here, look at this material—it looks promising,'” said University of Chicago Professor and Argonne senior scientist Giulia Galli, a co-author of the study and Q-NEXT collaborator. “We are after new qubit platforms, new materials. Identifying mathematical relationships like this one points out new materials to try, to combine.”
With this equation in hand, the researchers plan to boost the accuracy of their model.
They’ll also connect with researchers who can create the materials with the most promising coherence times, testing whether they perform as well as the equation predicts. (The team has marked one success already: A scientist outside the team reported that the relatively long coherence time of a material called calcium tungstate performed as predicted by the team’s formula.)
“Our results help us with advancing current quantum information technology, but that’s not all,” said Tohoku University Professor Hideo Ohno, who is currently president of the university and paper co-author. “It will unlock new possibilities by bridging the quantum technology with a variety of conventional systems, allowing us to make even greater progress with the materials we’re already familiar with. We’re pushing more than one scientific frontier.”
A three-qubit entangled state has been realized in a fully controllable array of spin qubits in silicon
Shun Kanai et al, Generalized scaling of spin qubit coherence in over 12,000 host materials, Proceedings of the National Academy of Sciences (2022). DOI: 10.1073/pnas.2121808119
Citation:
A mathematical shortcut for determining quantum information lifetimes (2022, April 6)
retrieved 7 April 2022
from https://phys.org/news/2022-04-mathematical-shortcut-quantum-lifetimes.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no
part may be reproduced without the written permission. The content is provided for information purposes only.
